Network Effects And Cascading Behaviour

The phenomenon of spreading through networks and cascading behaviors is prevalent in a wide range of real networks. Examples include contagion of diseases, cascading failure of technologies, diffusion of fake news, and viral marketing. Formally, an “infection” event can spread contagion along main players (active/infected nodes) which constitute a propagation tree, known as a cascade. In this section, we study how a infection propagates through a network. We will look into two classed of model, namely decision based models and probabilistic models. But first lets look at some terminology used throughout the post.

Terminology

Cascade: Propagation tree created by spreading contagion
Contagion: What is spreading in the network, e.g., diseases, tweet, etc.
Infection: Adoption/activation of a node
Main players: Infected/active nodes, early adopters

Decision Based Models

In decision based models, every nodes independently decides whether to adopt the contagion or not depending upon its neighbors. The decision is modelled as a two-player coordination game between user and its neighbor and related payoffs. Hence a node with degree $k$ plays $k$ such games to decide its payoff and correspondingly its behavior.

Single Contagion Model

There are two contagions $A$ and $B$ in the network and initially every node has behavior $B$ . Every node can have only one behavior out of the two. The payoff matrix is given as:

	A	B
A	a	0
B	0	b

Lets analyze a node with d neighbors, and let p be the fraction of nodes who have adopted $A$ . Hence the payoff for $A$ is $apd$ and payoff for $B$ is $b(1-p)d$ . Hence the node adopts behavior $A$ if $apd > b(1-p)d \implies p > \frac{b}{a+b} = q$ (threshold)

Key Insights:

Uniform activation threhold for users, with two peaks
Most cascades are short
Successful cascades are started by central users

Note:

k-core decomposition: biggest connected subgraph where every node has at least degree k (iteratively remove nodes with degree less than k)

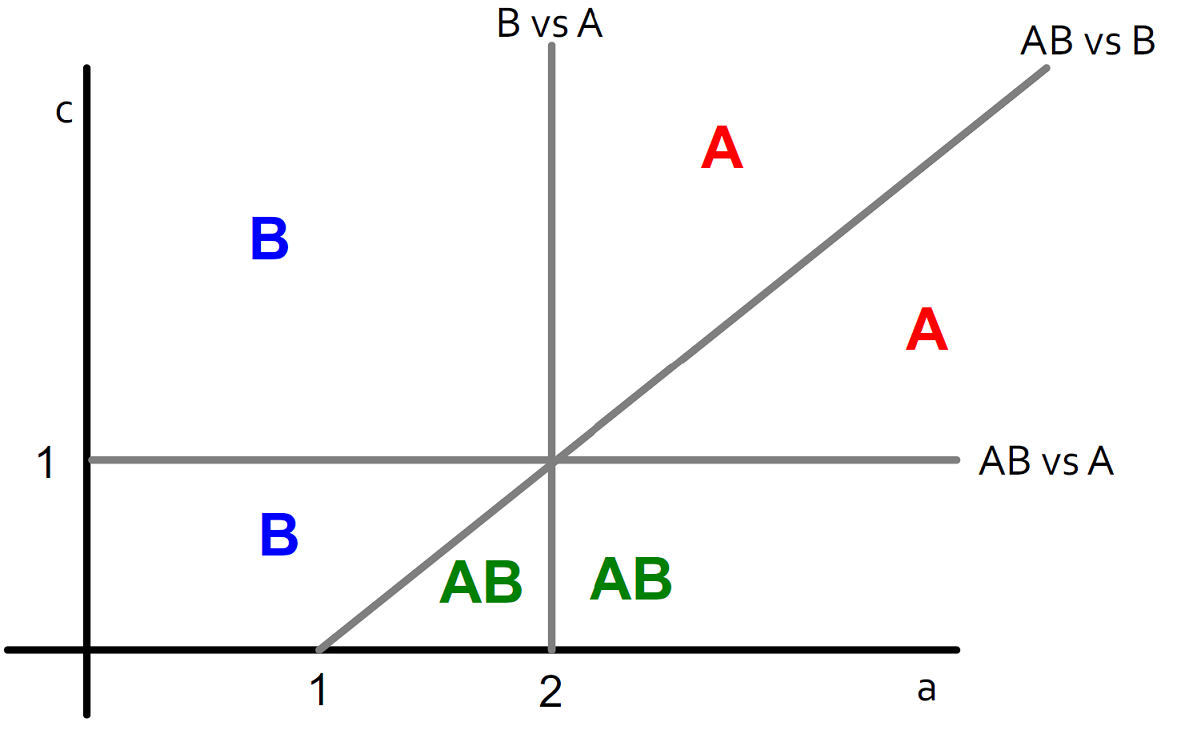
Multiple Contagion Model

There are two contagions $A$ and $B$ in the network and initially every node has behavior $B$ . In this case a node can have both behavior $A$ and $B$ at a total cost of $c$ (over all interactions). The payoff matrix is given as:

	A	B	AB
A	a	0	a
B	0	b	b
AB	a	b	max(a,b)

Example: Infinite Line graph

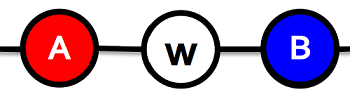
Case 1:A-w-B decision_case_1

Payoffs for $w$ : $A: a$ , $B: 1$ , $AB: a+1-c$

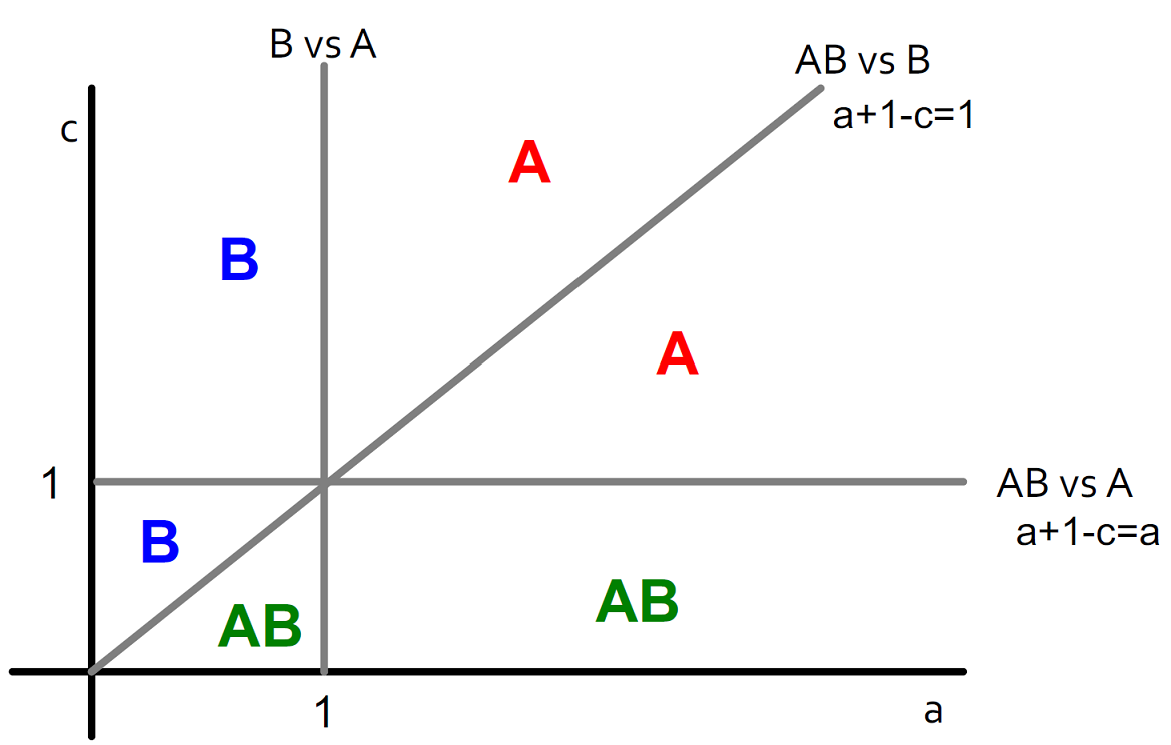
decision_case_2

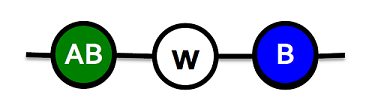
Case 1: AB-w-B decision_case_3

Payoffs for $w$ : $A: a$ , $B: 1$ , $AB: max(a, 1) + 1 -c$

decision_case_4